Slow Particles
Slow Particles
In the issues we found that it is necessary to keep the speed, the distance moved per frame, of particles to below, twice the radius of a particle, to ensure they intersect with walls or each other. Slow particles are those where the initial speed meets this restriction. When the resultant velocities after the collision are based on Newtonian physics for perfectly elastic particles then there are situations when the speeds of particles can increase to indefinitely.
The Collisions
For Newtonian physics -
When a particle hits the wall then its velocity perpendicular to the wall will be reversed.
When two particles collide their velocities along the line joining their centres are exchanged and they retain their velocities tangential to this line.
Under the right circumstances it is possible for the speed of a number of particles to all be given additively to one particle.
In Fig 14 the positions of the four pink particles are shown as at frame 1. Each with a radius r and speed v, their velocities shown by the blue arrows. Their positions at frame 2 are shown in grey. At frame 3 the dark grey particles have moved to the red positions, each now having a speed of 2√v. By frame 4 the darker red particle has moved to the position shown in purple now with a speed of 2v. So if the particles had started with a velocity of 0.6r by the fourth frame the verticle speed of one of the particles will be 2.4r, fast enough to avoid intersection with a wall or another sphere.
Given that the dark red particles reaches position (x, y, 0) when its speed reaches twice the velocity of the pink particles then the necessary positions for their start are shown in Fig 15.
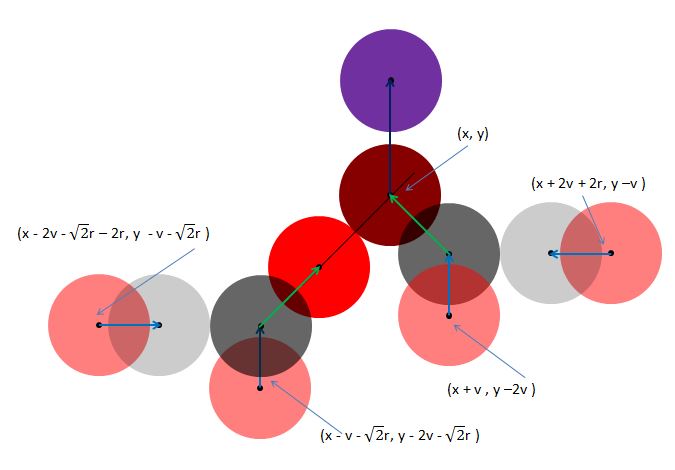Fig 15
The following Playgrounds use four such sets of particles, to produce four particles that combine to give one particle a speed four times that of the original particles. In each case the higher two groups are set in the XY plane and the lower two groups are in the YZ plane.
Playground Example - Increasing Speed -
Playground Example - Increasing Speed With Trail Markers per Frame -
Playground Example - Increasing Speed, More Spacing -
Escaping Particles
In the above examples the four fold increase in speed depended on setting the particles in particular positions. In the case of randomly positioning particles, with random velocities, in a box then it is less likely that this will happen but it is possible.
In the Playground below, there are occassions when particles escape the box even though there initial speeds are set to below 2r. You may need to run the code more than once to see the effect.
Playground Example - Escaping Particles -
The maximum speed of the particles can be changed on lines 21 to 23. Lowering the values for the speed decreases the probabilty of escape.
A single red particle is included so that its reaction can be followed.
Stopping the Escapes
The easiest way to stop the particles escaping is to rebound from a wall if the displacement of a particle is less than the radius. Any particle that is close enough to the wall will rebound, as will any particle that passes through the wall since its displacement from the wall will be negative and so must be less than the radius.
Making no changes to the intersection between particles means there can be times that particles will pass through each other. A high number of particles means that this is not noticeable.
The following Playground is an example that uses the above method to stop particles escaping. One downside is that particles can be seen breaching the walls.
Playground Example - No Escaping Particles -
The maximum speed of the particles can be changed on lines 21 to 23.
A single red particle is included so that its reaction can be followed.
Conclusion
To produce a system of collisions using Newtonian physics the path of a particle between frames must be determined.