Free Particles

After considering the issues involved and slow slow particles we are now ready to consider free particles, ones that move with no restriction to their start position or velocity.

The velocity of a particle is its displacement per frame.

Colliding with a Wall

Given a particle of radius r, at position p and velocity v in frame n, the particle will collide with a wall when it is travelling towards the wall in frame n and in frame n+1 the centre of the particle, at p + v, is within a distance r from the wall or is moving away from the wall.

For example consider a left hand wall, with plane parallel to the YZ plane, and a particle travelling towards it with velocity (dx, dy, dz), dx < 0.

In frame n, the position of the particle is (x, y, z) and during the time between frame n and frame n+1 it overlapped the wall. At frame n+1, the particle may still be overlapping the wall and its centre may be to the right or left of the wall or, the particle may have gone beyond the wall completely. The 2D diagrams show the latter case but the calculations apply in all cases. Fig 16 indicates the particle passing through the wall.

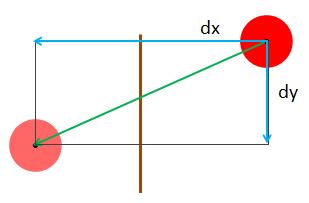
     Fig 16.

The particle at frame n+1, is at position (x + dx, y + dy, z + dz)

Sometime between frame n and frame n+1 the particle would just touch the wall as in Fig 17.

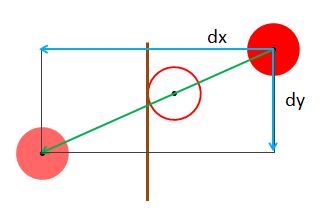
     Fig 17.

At this position let the displacement of the particle from its position in frame n be (dx₁, dy₁, dz₁) and its displacement from this position to its position in frame n+1 be (dx₂, dy₂, dz₂). It follows that (dx, dy, dz) = (dx₁, dy₁, dz₁) + (dx₂, dy₂, dz₂), see Fig 18.

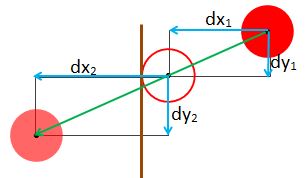
     Fig 18.

At the point of contact with this wall the component of velocity in the x direction would reverse and so the remaining x axis displacement before frame n+1 would be -dx₂, see Fig 19.

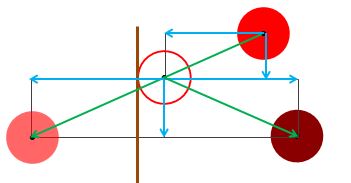
     Fig 19.

The particle velocity, after the collision is now (-dx, dy, dz). For frame n+1, we need the position of the particle to be at (x + dx₁ - dx₂ , y + dy, z + dz). Since before frame n+1, is displayed the velocity (-dx, dy, dz) will be added and so we need it position before this is done to be (x + dx₁ - dx₂ , y + dy, z + dz) - (-dx, dy, dz), see Fig 20.

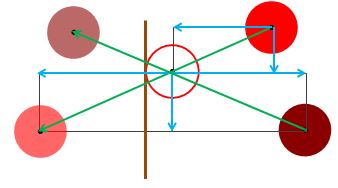
     Fig 20.

(x + dx₁ - dx₂ , y + dy, z + dz) - (-dx, dy, dz)

= (x + dx₁ - dx₂ + dx, y, z)

= (x + dx₁ - dx₂ + dx₁ + dx₂, y, z)

= (x + 2dx₁, y, z)

Which is the reflection of the particle at frame n in the plane parallel to the YZ plane through the centre of the particle, see Fig 21.

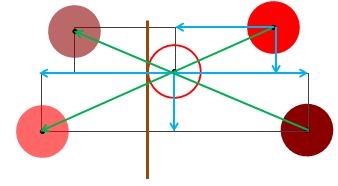
     Fig 21.

This means after frame n is displayed the particle's position has to be reset as indicated.

Colliding Particles

Given a two particles P and Q of radius r, at positions p and q with velocities v and u repectively travelling towards each other in frame n. In frame n+1 the centres of the particle are at p + v and q + u. Between frame n and frame n+1* the two particles would collide when there is a time t <= 1 when the distance between the positions of the particles is 2r. See Fig 22.

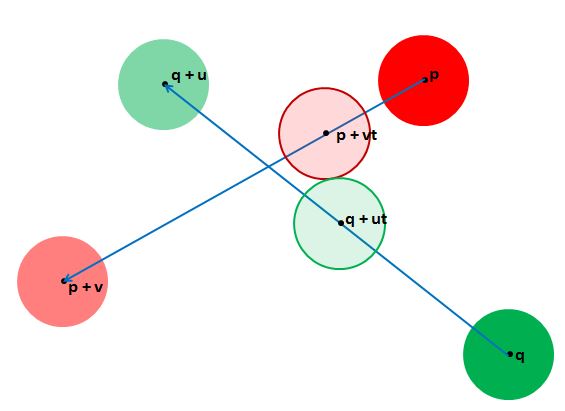
     Fig 22.

At time t, P is at p + vt and Q is at p + ut and P an Q will collide if there is a solution for t to the equation

(p + vt - (q + ut)).(p + vt - (q + ut)) = 4r²

with 0 < t <= 1

This equation is a quadratic equation in t of the form at² + bt + c = 0

(p + vt - (q + ut)).(p + vt - (q + ut)) = 4r²

(p - q +(v - u)t).(p - q +(v - u)t) = 4r²

(p - q).(p - q) + 2(p - q).(v - u)t + (v -u).(v - u)t² = 4r²

(v -u).(v - u)t² + 2(p - q).(v - u)t + (p - q).(p - q) - 4r²

so a = (v -u).(v - u), b = 2(p - q).(v - u), c = (p - q).(p - q) - 4r²

There will be a collision between frame n and frame n+1 provided b² - 4ac > 0. In this case there will be two solutions for t the smallest value being where the particles first touch and the other at the end of the overlap.

Based on the above the following Playground shows two spheres and their paths. Should they collide their positions at first touch are shown. Their start positions and velocities may be set at lines 35 to 38.

Playground Example - First Contact -

.

Reaction

Since only the velocities along the line joining the centres of the particles are affected during the collision we need to consider axes along this radial line and a tangential line. The particles are at first contact at time t, with P at p + vt and Q at q + ut

Let m = p + vt - (q + ut) and n = m/|m| a unit vector.

Then v_r = (v.n)n is the component of v along n, and u_r = (u.n)n the component of u along n and after collision these components are swapped. The tangential components for P and Q before collision are v_t = v - (v.n)n and u_t = u - (u.n)n respectively.
After collision the velocity of
P is v_a = u_r + v_t = (u.n)n + v - (v.n)n = v + ((u - v).n)n and that of
Q is u_a = v_r + u_t = (v.n)n + u - (u.n)n = u + ((v - u).n)n

Given that the particles collide between frame n and frame n+1 what will the positions of P and Q be during frame n+1?

In frame n, the position of particle P is (px, py, pz) and the position of Q is (qx, qy, qz). For some time t <= 1 the particles will make first contact. Fig 23 shows the positions of P and Q for frame n, their positions at time t, and their positions for frame n+1 when the collision is not detected. The radial and tangential components of their displacements (= velocities) are also shown upto and after first contact.

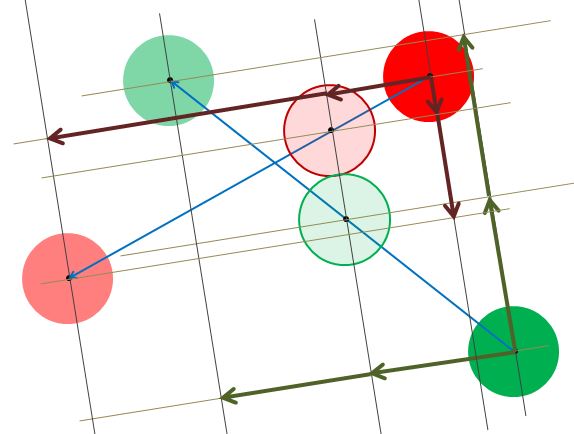
     Fig 23.

The displacement v can be split in vt and v(1 - t) and u can be split into u and u(1 - t) which take the particles to the point of contact and after the first contact. During the frame transition it is at the point of contact the displacements along the line of centres are exchanged.

Fig 24 shows the rearrangement of the component displacements and positions of the spheres when the collision is detected and component velocities along the line joining the centres are exchanged. Just before frame n+1 this gives

particle P at p + v_rt + v_tt + u_r(1 - t) + v_t(1 - t) = p + v_rt + u_r(1 - t) + v_t and particle Q at q + u_rt + u_tt + v_r(1 - t) + u_t(1 - t) = q + u_rt + v_r(1 - t) + u_t
as in Fig 24

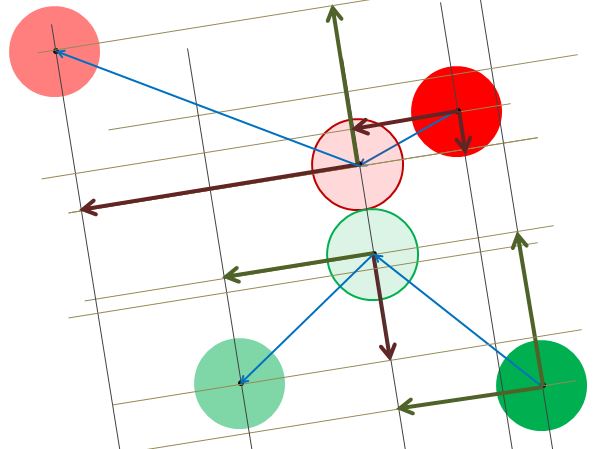
     Fig 24.

However, since before frame n+1, is displayed the velocities of P and Q will be added to the positions of P and Q and so we need these positions to have their velocities subtracted so that the correct positions are displayed during frame n+1. See Fig 25

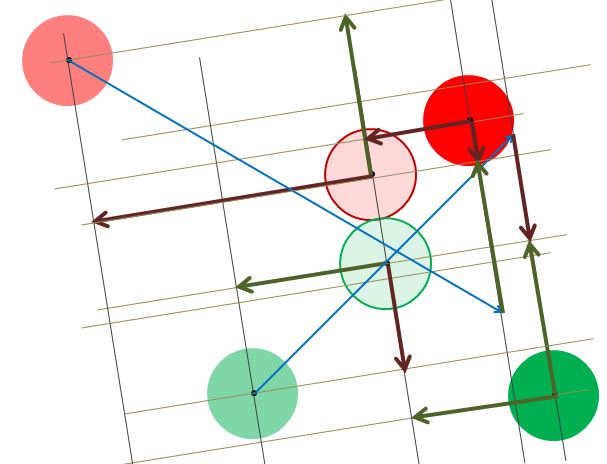
     Fig 25.

P
p + v_rt + u_r(1 - t) + v_t - (u_r + v_t)

= p + v_rt + u_r(1 - t) - u_r

= p + v_rt + u_r(1 - t) - u_rt - u_r(1 - t)

= p + v_rt - u_rt

= p + (v_r - u_r)t

Q
q + u_rt + v_r(1 - t) + u_t - (v_r + u_t)

= q + u_rt + v_r(1 - t) - v_r

= q + u_rt + v_r(1 - t) - v_rt - v_r(1 - t)

= q + u_rt - v_rt

= q + (u_r - v_r)t

After a collision these values are used to recalculate the positions of particles before frame n+1.

The following Playground shows the first contact position of two particles and their paths before and after collision. Start position and velocities may be set on lines 36 to 39.

Playground Example - First Contact Rebound -

.

This Playground fires particles randomly towards each other to see the effect when they collide.

Playground Example - Colliding Particles -

.

A Multitude of Particles

Combining all of the above the following Playgrounds put many particles inside a box and have them collide with the box and each other.

Playground Example - Slow Moving Particles -

Playground Example - Fast Moving Particles -

Maximum speeds, for both, can be changed on lines 21 to 23.

Further Reading

Slow Particles