Frames of Reference

There are two frames of reference that BabylonJS uses with a mesh, the world axes and the local axes. In all diagrams and playgrounds X axis is red, Y axis is Green and Z axis is blue. In all examples a non symmetrical mesh, the pilot, will be used.

The Pilot

When the pilot is created its position and rotation are both set to (0, 0, 0), its scaling to (1, 1, 1) and all frames of reference coincide.

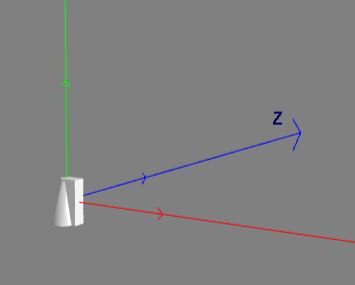
Position

Position places the pilot with reference to the word axes using a vector (x, y, z). The local axes move with the pilot.

pilot.position = new BABYLON.Vector3(2, 3, 4);

or individual components

pilot.position.x  =  2;
pilot.position.y  =  3;
pilot.position.z  =  4;

The local and world axes remain in the same orientation.

Playground Example for Position -

Rotation

WARNING Rotating in 3D space is always tricky. The order in which rotations are applied to a shape changes the final orientation of the shape and there are many varying conventions for applying rotations. For more details on these conventions in Babylon JS see Applying Rotations Convention BJS

In BabylonJS

Rotations are set using

 pilot.rotation = new BABYLON.Vector3(alpha, beta, gamma);

or

pilot.rotation.x  =  alpha;
pilot.rotation.y  =  beta;
pilot.rotation.z  =  gamma;

with the following conventions

All rotations are in radians and are anticlockwise when looking in the direction of the positive axes.

Rotation turns about the centre of rotation at the origin of the local axes and rotation with reference axes parallel to the world axes using a vector ( alpha, beta, gamma) or individual components. Where alpha is the rotation about the x axis, beta about the y axis and gamma about the z axis.

Rotations are always applied in the order z, x, y whether set as a single vector or individually.

The following all produce the same orientation

pilot.rotation = new BABYLON.Vector3(alpha, beta, gamma);

pilot.rotation.x  =  alpha;
pilot.rotation.y  =  beta;
pilot.rotation.z  =  gamma;

pilot.rotation.z  =  gamma;
pilot.rotation.x  =  alpha;
pilot.rotation.y  =  beta;

pilot.rotation.y  =  beta;
pilot.rotation.z  =  gamma;
pilot.rotation.x  =  alpha;

The following diagrams show that applying a rotation of PI/2 in the axis order, z, x, y or y, x, z give the same result.

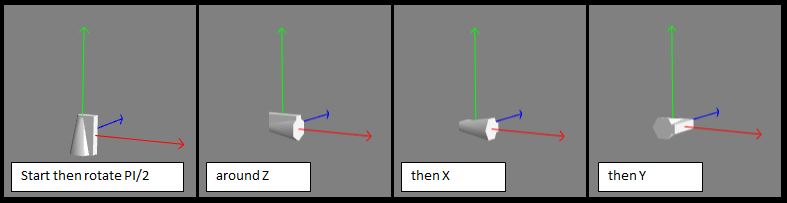
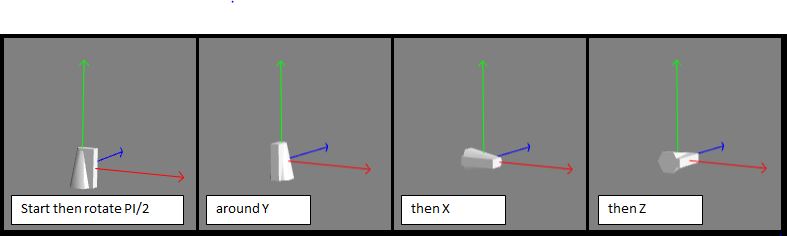
This consistency of order z, x, y can be further checked out in the following playground by re-ordering and/or commenting out lines 38, 39 and 40

Playground Example for Rotation -

Simple Animation using Position and Rotation

The aim is to produce an animation of a disc rotating along a straight horizontal path. When a disc of radius r rotates through an angle theta the disc travels a distance of r * theta. For the animation this means a series of positions a distance r * theta apart. These positions are used as the points with which to create the line.

Playground Example Rotation Along Straight Horizontal Path -

Further Reading

Rotate about Axis
Rotate a Mesh
Applying Rotations Convention BJS