Facet Normals
Facet Normals
For an individual facet BabylonJS computes its normals as mathematical normals, at right angle to the facet. However there is no necessity for them to be set at right angles. In the following two playgrounds see how the changing directions within the normals array affect how it is lit.
Playground Example Showing Normals Varying in Unison -
Playground Example Showing Normals Varying -
Normals and Minimum Vertices
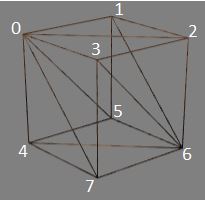
The box above has 8 vertices. If we want to keep the indices to the minimum they will be 0, 1, 2, 3, 4, 5, 6, 7. Facets 0, 3, 7 and 3, 7, 6 and 0, 3, 2 all have vertex 3 in common and vertex 3 can only have one entry in the normals array associated with it. How does BabylonJS calculate the 'normal' for vertex 3? The diagram below shows that the average of the three mathematical normals at each vertex is used.
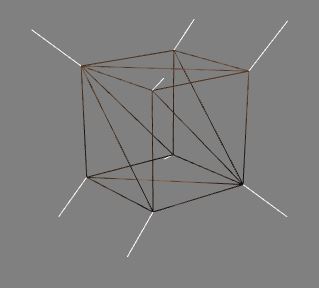
NOTE each of the triples in the normals array is often referred to as a normal even though they are not strictly speaking the mathematical normal.
Besides minimising the number of vertices needed there are other advantages as will be seen when creating a sphere.
Table of Indices, Positions and Normals for Box with Minimum Vertices
| index | position | normal |
|---|---|---|
| 0 | ( -1 , 1 , -1 ) | ( -0.5773502691896258 , 0.5773502691896258 , -0.5773502691896258 ) |
| 1 | ( 1 , 1 , -1 ) | ( 0.8164965809277261 , 0.4082482904638631 , -0.4082482904638631 ) |
| 2 | ( 1 , -1 , -1 ) | ( 0.4082482904638631 , -0.4082482904638631 , -0.8164965809277261 ) |
| 3 | ( -1 , -1 , -1 ) | ( -0.4082482904638631 , -0.8164965809277261 , -0.4082482904638631 ) |
| 4 | ( -1 , 1 , 1 ) | ( -0.4082482904638631 , 0.4082482904638631 , 0.8164965809277261 ) |
| 5 | ( 1 , 1 , 1 ) | ( 0.4082482904638631 , 0.8164965809277261 , 0.4082482904638631 ) |
| 6 | ( 1 , -1 , 1 ) | ( 0.5773502691896258 , -0.5773502691896258 , 0.5773502691896258 ) |
| 7 | ( -1 , -1 , 1 ) | ( -0.8164965809277261 , -0.4082482904638631 , 0.4082482904638631 ) |
Normals and Flat Shaded Meshes.
There are times, such as needing each face of a box to be covered in a different material, when it is better to have the box constructed from seperate faces each of which are contructed by two facets and no two faces sharing a vertex indices. They will of course share vertex positions.
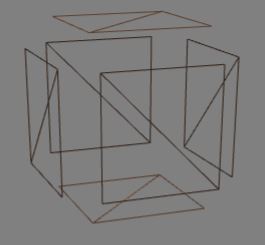
In BabylonJS this can be achieved using the convertToFlatShadedMesh function. The results are shown below.

Table of Indices, Positions and Normals for Flat Shaded Box
| index | position | normal |
|---|---|---|
| 0 | ( -1 , 1 , -1 ) | ( 0 , 0 , -1 ) |
| 1 | ( 1 , -1 , -1 ) | ( 0 , 0 , -1 ) |
| 2 | ( 1 , 1 , -1 ) | ( 0 , 0 , -1 ) |
| 3 | ( -1 , 1 , -1 ) | ( 0 , 0 , -1 ) |
| 4 | ( -1 , 1 , 1 ) | ( 0 , 0 , 1 ) |
| 5 | ( 1 , -1 , 1 ) | ( 0 , 0 , 1 ) |
| 6 | ( -1 , -1 , 1 ) | ( 0 , 0 , 1 ) |
| 7 | ( -1 , 1 , 1 ) | ( 0 , 0 , 1 ) |
| 8 | ( 1 , 1 , -1 ) | ( 1 , -0 , 0 ) |
| 9 | ( 1 , -1 , 1 ) | ( 1 , -0 , 0 ) |
| 10 | ( 1 , 1 , 1 ) | ( 1 , -0 , 0 ) |
| 11 | ( 1 , 1 , -1 ) | ( 1 , 0 , 0 ) |
| 12 | ( -1 , 1 , -1 ) | ( -1 , 0 , 0 ) |
| 13 | ( -1 , -1 , 1 ) | ( -1 , 0 , 0 ) |
| 14 | ( -1 , -1 , -1 ) | ( -1 , 0 , 0 ) |
| 15 | ( -1 , 1 , -1 ) | ( -1 , -0 , -0 ) |
| 16 | ( -1 , 1 , -1 ) | ( 0 , 1 , 0 ) |
| 17 | ( 1 , 1 , 1 ) | ( 0 , 1 , 0 ) |
| 18 | ( -1 , 1 , 1 ) | ( 0 , 1 , 0 ) |
| 19 | ( 1 , 1 , -1 ) | ( 0 , 1 , -0 ) |
| 20 | ( -1 , -1 , -1 ) | ( 0 , -1 , -0 ) |
| 21 | ( 1 , -1 , 1 ) | ( 0 , -1 , -0 ) |
| 22 | ( 1 , -1 , -1 ) | ( 0 , -1 , -0 ) |
| 23 | ( -1 , -1 , 1 ) | ( 0 , -1 , 0 ) |
Playground Showing Box Normals
Playground Example for Box Normals -
Advantage of Shared Normals
Sharing normals means that the shader produces a rounder looking sphere. Applying the function converToFlatShadedMesh shows the individual faces making up the sphere.
Playground Example Comparing Shading of Spheres -