Collision Issues

Checking for an Intersect

One way to check in BabylonJS whether two meshes are colliding is to use the intersectsMesh method. So for Fig 1

sphere.intersectsMesh(wall)

would give the result true

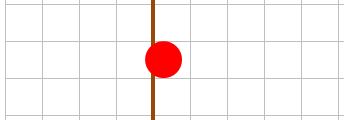
     Fig 1

You may think that where the sphere in Fig 2 is travelling towards the wall that you could use

if(sphere.intersectsMesh(wall)) {
    //bounce sphere off wall
}
else {
    //move sphere left
}

     Fig 2

However consider the sphere as having unit diameter and is moving towards the ball with a speed of 5 units per frame. The check for collision has to be considered for each frame. The first frame is as in Fig 3 and the next frame as in Fig 4

     Fig 3

The sphere will have gone past the wall and is not intersecting it and so no collision will be detected

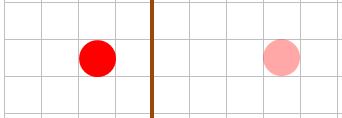
     Fig 4

Size and Speed Matter.

Consider a sphere of radius r travelling towards a wall with speed v, at a position just out of contact with the wall. To be able definitely to use of the intersectsMesh method the sphere must be in contact with the wall during the next frame. The maximum distance the sphere can travel between frames must be less than twice the radius, as in Fig 5.

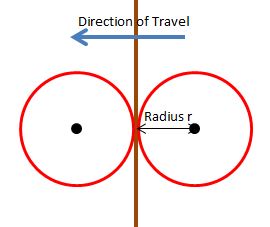
     Fig 5

So for the sphere to start in any random position and travel directly towards the wall and for an intersection with the wall definitely to take place during a frame v <= 2r

Now consider two spheres travelling towards each other, each sphere having a speed v. The relative velocity is 2v. Take one sphere as stationary and the other moving with speed v at a position just out of contact with each other. To be able to use the intersectsMesh method the spheres must be in contact with each other during the next frame. The maximum distance the moving sphere can travel between frames must be less than four times the radius, as in Fig 6.

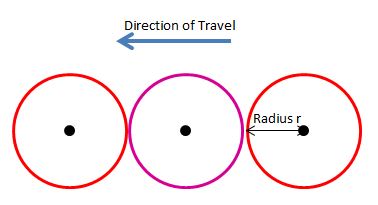
     Fig 6

So for two spheres to start in any random positions and travel directly towards each other and for an intersection with the wall definitely to take place during a frame 2v <= 4r, which is again v <= 2r.

To generalise , should one sphere have radius r₁ and speed v₁ and the other radius r₂ and speed v₂ intersections from random positions will definitely take place
when v₁ + v₂ < 2(r₁ + r₂)

What is the situation when v > 2r?

Consider that the front of the sphere is a distance d from the wall in a frame, F, and in the next frame, N, the sphere intersects the wall or has moved passed it, then 0 <= d <= v. If d > v then d - v > 0 and so in the next frame the sphere is still a distance d - v > 0 from the wall. In fact when the sphere is any distance p away from the wall, p > 0, then for frame F, d = p modulo v. Fig 7 shows that for the sphere to intersect the wall v - 2r < d V v.

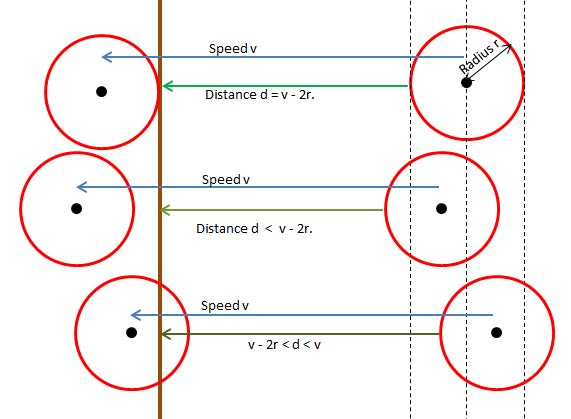
     Fig 7

The sphere just touches the wall when d = 0 and so for a display where the sphere does not penetrate the wall p modulo v is 0.

Expressing this in quotient and remainder form p = qv, q >= 0

Since p is the distance from the front of the wall the centre of the sphere will be at qv + r.

Playground Example

In the following playground the three spheres are positioned so that for sphere1, d < v - r and so will pass through the wall; for sphere2 d = 0 and for sphere3 v - 2r < d < v. The radius and speed for each sphere have been set at the same values but can be changed easily should you wish to. Sphere1 is at the top, sphere2 the middle and sphere3 at the bottom.

Playground Example -

Hypotheses

Given a multitude of equally sized spheres, all initially inside a box and given random velocities and using Newtonian physics to inform the results of collisions

1. By setting the initial speed of each sphere to be twice the radius and contraining their initial positions to be within a grid system of cubes with size matching the diameter of the spheres then it is possible to create a system whereby all collisions and rebounds between a sphere and a wall and between two spheres take place when they just touch.

2. By setting the initial speed of each sphere to below twice the radius of a sphere then it is possible to form a system whereby all collisions and rebounds between a sphere and a wall and between two spheres can be detected by checking if the meshes intersect.

Both hypotheses turn out to be false. This can be seen by reading the following

1. Simple Particle Collisions on a Grid
2. Slow Particles

This being the case we turn to issues arising when the speed of a sphere is greater than twice the radius.

Stroboscopic Issues

What happens when the speed of a sphere is greater than twice the radius and you need to calculate its position following what should be a collision with the wall?

In Fig 8 the red arrow shows the movement of the sphere, between two frames, when the collision with the wall is not detected and the green arrow the required movement. The required position is a reflection, with the wall as reflector, of the through position.

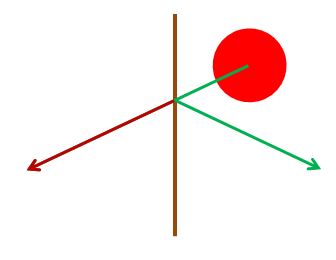
     Fig 8.

As usual r is the radius of the sphere.

Should a sphere be moving at right angles to a wall a distance 8r units from the wall and the speed of the sphere be 16r units then its reflected position will be its start position and the sphere will apper not to have moved. This is the stroboscopic effect.

The following Playground shows spheres all starting from a distance of 8r units from two walls, all moving at right angles to the walls with speeds ranging from 20r to 12r units.

Playground Example - Strobing -

Conclusion

Depending on the effect required it is probably better to start with speeds 2r or below per frame but even so it is not sufficient to use intersection of meshes to check for collisions and mathematical techniques will be needed. These techniques will both determine if collisions take place and the repositioning of the spheres.